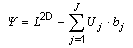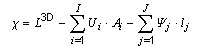Thermal Bridge Heat Transfer & Vapour Diffusion Simulation Program AnTherm Version 6.115 - 10.137

 [ ← ] [ ↑ ] [ → ] [ToC]

Basics and Some Theory of AnTherm

Linear and Point Thermal Transmittance

Often thermal bridges will be described in terms of linear and point thermal transmittances characteristic to building components analysed.

 

linear thermal transmittance, Ψ

[W/mK]

Psi

 heat flow rate in the steady state divided by length and by the temperature difference between the environments on either side of a thermal bridge (definition in ISO 10211)
NOTE The linear thermal transmittance is used as a correction term for the linear influence of a thermal bridge.

The linear thermal transmittance is given by:

where:

Ψ   is the linear thermal transmittance Psi of the linear thermal bridge separating the two environments being considered;
L2D   is the thermal coupling coefficient obtained from a 2-D calculation of the component separating the two environments being considered;
Uj   is the thermal transmittance of the 1-D component j separating the two environments being considered;
bj   is the length within the 2-D geometrical model over which the value Uj applies
J   is the number of 1-D components.

Note: When determining the linear thermal transmittance, it is necessary to state which dimensions (e.g. internal or external) are being used because for several types of thermal bridges the value of the linear thermal transmittance depends on this choice.

 
point thermal transmittance, χ

[W/K]

chi

 heat flow rate in the steady state divided by the temperature difference between the environments on either side of a thermal bridge (definition in ISO 10211)
NOTE The point thermal transmittance is used as a correction term for the influence of a point thermal bridge.

The point thermal transmittance is given by:

where:

χ   is the point  thermal transmittance Chi of the point thermal bridge separating the two environments being considered;
L3D   is the thermal coupling coefficient obtained from a 3-D calculation of the 3-D component separating the two environments being considered;
Uj   is the thermal transmittance of the 1-D component j separating the two environments being considered;
Aj   is the area over which the value Uj applies;
Ψj   are respective linear thermal transmittances (see above);
lj   is the length over which the value Ψj applies;
J   is the number of 2-D components.
I   is the number of 1-D components.

Note: When determining Ψ and χ values, it is necessary to state which dimensions (e.g. internal or external) are being used because for several types of thermal bridges the Ψ and χ values depend on this choice..

Rewriting the above equation by replacing the linear thermal transmittance by its definition, provides following alternative means of calculating the point thermal transmittance:

 

 

An alternative expression for the total coupling coefficient Li,j which uses the linear and point thermal transmittances, Ψ and χ , is then given by

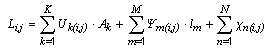
where:

Uk(i,j)   is the thermal transmittance of part k of the room or building;
Ak   is the area over which the value Uk(i,j) applies;
Ψm(i,j)   is the linear thermal transmittance Psi of part m of the room or building;
lm   is the length over which the value Ψm(i,j) applies;
χn(i,j)   is the point thermal transmittance Chi of part n of the room or building;
K   is the number of thermal transmittances.
M   is the number of linear thermal transmittances;
N   is the number of point thermal transmittances;

Note: In above formula ΣAk is equal to the total surface area of the envelope.

Note: Li,j is equivalent to the heat transfer coefficient, H often used in other standards.

See also: Conductance , On calculation of Ψ-values for building constructions in connection with ground, Theoretical background

 Model, Calculate, Simulate and Analyse Thermal Heat Bridges in 2D and 3D with AnTherm®  

[ ← ] [ ↑ ] [ → ] [ToC] 
 Copyright © Kornicki Dienstleistungen in EDV & IT